Agronomía Tropical. 49(3):297-325. 1999

DEFINICIÓN DE PATRONES HOMOGÉNEOS DE PLUVIOSIDAD EN 
LOS LLANOS CENTRALES VENEZOLANOS 
MEDIANTE KRIGING FACTORIAL

Rebeca Pradere G.

Profesora. Universidad Central de Venezuela. Facultad de
Ingeniería. Departamento de Matemáticas Aplicadas. Cagua 2122.
Estado Aragua. Venezuela. 

RECIBIDO: mayo 04, 1998

RESUMEN

La clasificación es importante para comprender los factores que afectan los patrones climáticos y permite mejorar la planificación de actividades dependientes del clima. La precipitación puede considerarse la realización de un proceso aleatorio espacio-temporal cuyas estructuras de variabilidad pueden explorarse mediante técnicas estadísticas apropiadas para analizar datos espaciales multivariados y multiescalares. El propósito del trabajo fue definir patrones de pluviosidad mediante la aplicación de un Análisis de Kriging Factorial (AKF) a datos de precipitación registrados por el MARNR durante 1968-1983 en 55 puestos pluviométricos de los llanos centrales venezolanos. Un Análisis de Componentes Principales (ACP) aplicado a V, la matriz de varianza-covarianza de los promedios mensuales de precipitación, permitió identificar tres fuentes de variabilidad espacial: la estación lluviosa, el cambio de estación y la sequía. Ajustando un Modelo Lineal de Corregionalización a los doce promedios mensuales de precipitación se descompuso V en tres matrices de corregionalización B^u, u = 1,2,3, asociadas, respectivamente, a un efecto nugget y a dos esquemas esféricos con rangos de 65 000 y 140 000 UTM. El ACP de las matrices B^u permitió apreciar en la estación lluviosa la influencia del efecto nugget y de la escala de 65 000 UTM; las épocas de sequía y transición lluvia-sequía parecieron influenciadas por el rango de 140 000 UTM, y la escala de 65 000 UTM dominó la transición sequía-lluvia. El valor de los dos primeros factores regionalizados estimados mediante cokriging en los puntos muéstrales generó una clasificación de los puestos pluviométricos en función de la escala espacial. 

Palabras clave: precipitación, análisis de componentes principales, Geoestadística, datos espaciales multivariados, kriging factorial, llanos, Venezuela.

SUMMARY

INTRODUCCIÓN

La precipitación, al igual que otras variables climáticas, puede considerarse la realización de un proceso espacio-temporal porque exhibe aspectos aleatorios tanto en el tiempo como en el espacio. Si la dependencia espacial resulta más importante, la estimación espacio-temporal se puede simplificar integrando el componente temporal y reduciendo el problema a una interpolación en el espacio. Por otra parte, en las variables climáticas es común que los mecanismos de variación operen a diferentes escalas espaciales y temporales (White et al., 1991), y una herramienta adecuada de análisis debe explorar esa condición para proporcionar una mejor descripción de los factores que gobiernan la variación.

Las técnicas geoestadística modelan la estructura de variabilidad de los datos mediante un semivariograma, y la técnica de estimación se conoce como kriging. Desde su primera formulación (Matheron, 1971) esta metodología ha encontrado aplicación en múltiples campos. En el caso multivariado, la herramienta de análisis estructural se extiende del semivariograma simple al semivariograma cruzado. La técnica de estimación se denomina cokriging (Journel y Huijbregts, 1978; Myers, 1982; Wackernagel, 1995). Los trabajos de Solow y Gorelick (1986) y Hevesi et al. (1992a,b) muestran algunas aplicaciones de la geoestadística multivariada al estudio de variables pluviométricas.

El Análisis de Kriging Factorial se fundamenta en el ajuste de un Modelo Lineal de Corregionalización (MLC) que modela todos los semivariogramas simples y cruzados como combinación lineal de S funciones básicas, una para cada escala de variación evidenciada por los datos. Este enfoque permite descomponer la matriz de varianza-covarianza en S matrices de corregionalización, y aplicar una técnica multivariada adecuada para explorar la estructura de correlación correspondiente a cada escala.

Myers (1982) propone deducir el modelo de covariograma como combinación lineal de modelos de semivariograma simple previamente ajustados, y chequear la validez del ajuste verificando el cumplimiento de la desigualdad de Cauchy-Schwarz. Wackernagel (1989) utiliza este método en un programa de computación desarrollado para analizar datos multivariados con distribución espacial. Sin embargo, el procedimiento puede producir varianzas negativas e inestabilidad numérica (Goovaerts, 1994). Goulard y Voltz (1992) describen un procedimiento automatizado para ajustar un MLC matemáticamente apropiado, e indican cómo reducir el número de parámetros del modelo matricial de covariograma para incrementar la estabilidad del ajuste.

Las ventajas del AKF para analizar información espacial multivariada son ilustradas por Goovaerts (1992) al comparar los resultados de un Análisis de Componentes Principales a la clásica matriz de varianza-covarianza, a las matrices de semivariograma y a las matrices de corregionalización para varios conjuntos de datos sintéticos y reales. Sólo el análisis de estas últimas permite apreciar cómo varía la estructura de correlación de una escala a otra. El AKF proporciona, además, un conjunto de factores regionalizados que resumen las principales características de los datos para cada escala de variación.

La superioridad del AKF sobre el análisis multivariado clásico para diferenciar efectos puntuales, locales y regionales se puede apreciar también en los trabajos de Wackernagel y Butenuth (1988) y Goovaerts et al. (1993).

Goovaerts (1993) estudia la ortogonalidad espacial de los Componentes Principales (CP) calculados a partir de variables corregionalizadas para diferentes situaciones y estructuras de correlación. En algunos casos se encuentra que la correlación entre los CP puede no ser despreciable a distancias cortas, especialmente cuando la estructura de correlación cambia con la escala. En un caso se logra reducir la correlación espacial entre algunos CP mediante una rotación ortogonal con criterio varimax de los primeros componentes.

En el presente trabajo se planteó identificar las principales fuentes de variabilidad de la precipitación y detectar la presencia de patrones homogéneos de pluviosidad en los llanos centrales venezolanos a partir de datos de precipitación registrados por el MARNR en la zona. 

Como los fenómenos ambientales suelen ser multiescalares, se exploró la presencia de más de una escala de variación con el propósito de identificar el alcance espacial de las estructuras más influyentes relacionadas con el patrón de precipitación. El rango de correlación espacial de las distintas fuentes de variabilidad identificadas, así como la distribución de los puestos pluviométricos donde la precipitación mensual promedio está dominada por una o más escalas particulares, podrían servir de referencia para un eventual rediseño de las redes de monitoreo que ajuste el muestreo espacial a la(s) escala(s) de la fuente de variabilidad más importante.

MATERIALES Y MÉTODOS

Para el desarrollo de la investigación se dispuso de promedios mensuales de precipitación calculados a partir de mediciones diarias registradas por el MARNR durante el lapso 1968-1983 en 55 puestos pluviométricos, localizados sobre un área rectangular de coordenadas planas limitadas por los intervalos [635 000; 945 000] UTM (longitud Oeste), y [840 000; 1 120 000] UTM (latitud Norte), región que abarca los llanos centrales venezolanos. La información en el espacio es escasa e irregular (ver Figuras 4, 5 y 6, más adelante). Como es común en el monitoreo de variables climáticas, la distribución de los puestos excluye extensas áreas poco pobladas y/o de difícil acceso.

Los fundamentos metodológicos del AKF (ver Goovaerts (1992), Goovaerts et al. (1993) y Wackernagel (1995)) son los siguientes:

Sea:

{z_i (xα); i = 1, 2,...., p; α = 1, 2, ..., N}            [1]

el conjunto de datos resultante de muestrear p variables regionalizadas Z_i (xα) en N puntos cuya posición está dada por el vector xα. De acuerdo con la Teoría de las Variables Regionailzadas (Matheron (1971), Journel y Huijbregts (1978)), las Z_i(xα) se pueden considerar una realización particular del conjunto de funciones aleatorias correlacionadas:

{Z_i (x); i = 1, 2, ...., p}                [2]

Sea Z(x) = [ Z₁ (x), Z₂ (x), ......, Z_p (x) ]. Bajo la hipótesis de estacionaridad de orden 2 se puede definir el vector de valores medios:

m = E [ Z (x) ] [3]

la matriz de covarianza:

C(h) = E { [ Z(x) - m ]^T [ Z(x+h) - m ] }            [4]

y la matriz de semivariograma:

Γ(h) = 1/2 E { [ Z(x) - Z(x+h) ]^T [ Z(x) - Z(x+h) ] }       [5]

Para un incremento h = 0, la matriz de covarianza es igual a la matriz de varianza-covariaza:

C(0) = E { [ Z(x) - m ]^T [ Z(x) - m ] } = V          [6]

Las matrices C(h) y Γ(h) dependen del incremento h (no de la posición x), y están relacionadas por la expresión:

Γ(h) = C(0) - 1/2 [ C(h) + C(-h) ]           [7]

En la práctica, la matriz Γ(h) se considera más útil que C(h) porque sólo impone el cumplimiento de la hipótesis de estacionaridad de segundo orden a los incrementos espaciales Z(x) - Z(x+h). Asumiendo que la correlación entre Z(x) y Z(x+h) desaparece cuando ׀h׀ → ∞, entonces C(h) →0 cuando ׀h׀ → ∞ y se deduce de [6] y [7] que:

Γ(h) → V si ׀h׀ → ∞                     [8]

La matriz de semivariograma experimental Γ(h) es una matriz simétrica p x p de elementos (h) que se calculan a partir de los datos en la forma:

   [9]

donde N_k es el número de pares increméntales considerados en la estimación correspondiente a un incremento h.

El Modelo Lineal de Corregionalización supone que el conjunto original de funciones aleatorias correlacionadas { Z_i (x); i = 1, 2, ..., p } se puede descomponer en un conjunto de funciones aleatorias no correlacionadas { Y_v^u (x); v = 1, 2, ...., p; u = 1, 2, ...., S } de la forma:

Z_i (x) =         10]

donde los Y_v^u son los factores regionalizados correspondientes a la u-ésima escala espacial y S es el número de escalas espaciales diferentes. Para un mismo índice u, las p funciones aleatorias Y_v^u (x) tienen la misma función de semivariograma g^u(h). Como los Y_v^u (x) son, por construcción, mutuamente ortogonales, se tiene que:

1/2 E { [ Y_v^u (x) - Y_v^u (x+h) ]^T [ Y_v'^u' (x) - Y_v'^u' (x+h) ] }

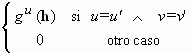=         [11]

de manera que los semivariogramas y_ij(h) se pueden expresar como combinación lineal de S funciones básicas g^u(h) en la forma:

y_ij (h) = 1/2 E { [ Z_i (x) - Z_i (x+h) ]^T [ Z_j (x) - Z_j (x+h) ] }

=

=

de forma que:

      [12]

donde:                                         [13]

En notación matricial, el modelo lineal de corregionalización de la ecuación [10] se puede escribir:

Z(x) =      [14]

donde Y^u (x) = [ Y₁^u (x) , Y₂^u (x) , ... Y_p^u (x) ], m = [ m₁, m₂, ..., m_p ] y A^u es la matriz de transformación [ a_iv^u ]. El modelo multivariado de semivariograma es:

[15]

donde Γ(h) es la matriz p x p de semivariogramas y B^u es la matriz de coeficientes b_ij^u conocida como matriz de corregionalización.

Para garantizar que las varianzas de todas las combinaciones lineales de las funciones aleatorias Z_i (x) sean positivas, la matriz Γ(h) debe ser condicionalmente semi-definida negativa, lo que se cumple si las g^u(h) son modelos autorizados de semivariograma y si cada matriz de corregionalización B^u = [ b_ij^u ], u=1, 2, ..., S, es semi-definida positiva. Esta última restricción implica el cumplimiento de las condiciones de Cauchy-Schwarz (necesarias pero no suficientes):

b_ii^u > 0 ; V i, u

 ׀ b_ij^u ׀ > ( b_ii^u b_jj^u )^1/2 ; V i, j, u   [16]

El significado de B^u se entiende mejor reescribiendo [14] en la forma:

[17]

donde los componentes Z_i^u(x) de Z^u(x) se denominan componentes espaciales, y representan el comportamiento de la función aleatoria Z_i(x) a una escala espacial u dada. Asumiendo estacionaridad de orden 2, su matriz de varianza - covarianza es la matriz B^u:

E [ (Z^u (x))^T Z^u (x) ] = E [A^u (Y^u (x))^T Y^u (x) (A^u )^T ] = A^u (A^u )^T = B^u   [18]

Cada matriz de corregionalización describe la relación entre las variables a la escala espacial definida por el rango de la correspondiente función básica g^u(h). Asumiendo estacionaridad de orden 2 y comportamiento asintótico de las funciones básicas g^u(h) (es decir, g^u(h) → 1 cuando ׀h׀ → ∞), se deduce de [8] y [15] que:

                                                                [19]

lo que significa que la estructura de correlación descrita por V es una mezcla de estructuras de correlación a diferentes escalas espaciales.

La descomposición de la matriz V en sus componentes principales se puede escribir:

          V = Q Λ Q^T = A A^T ; con A = Q Λ ^1/2           [20]

donde Q representa la matriz de autovectores, Λ la matriz diagonal de autovalores y A es la matriz p x p que transforma los componentes principales CPY_v(x) en las variables originales Z_i(x), de modo que:

       Z (x) = Y (x) A^T Λ Y (x) = Z (x) Q Λ^-1/2        [21]

con Y (x) = [ Y₁ (x), Y₂ (x), ..., Y_p (x) ] y [ Y (x) ]^T Y (x) = I.

De manera similar se puede aplicar un ACP para descomponer las matrices de corregionalización B^u en matrices de transformación A^u y resumir las relaciones entre las variables:

   B^u = A^u (A^u )^T Λ Y^u (x) = Z^u (x) Q^u (Λ^u) ^-1/2      [22]

En este último caso, las variables originales son los componentes espaciales Z_i^u(x) y los componentes principales son los factores regionalizados Y_v^u(x). Puesto que ambas variables son desconocidas, deben ser estimadas mediante cokriging. El estimador cokriging puede escribirse:

                                  [23]

donde p es el número de variables, n es el número de datos (alrededor de x_o) usados en la estimación y λαⁱ es el peso asignado al valor de la i-ésima variable en la a-ésima posición. Minimizando la varianza de estimación bajo la restricción de insesgamiento se obtiene un sistema de p x (n+1) ecuaciones lineales cuya solución proporciona los pesos ^λαi.

El comportamiento del fenómeno observado a diferentes escalas espaciales se puede apreciar mapeando los factores regionalizados Y_v^u(x) (o los componentes espaciales Z_i^u(x)). 

Sea:                                                      [24]

el estimador del factor regionalizado Y_v^u en el punto x₀. El correspondiente sistema de cokriging es:

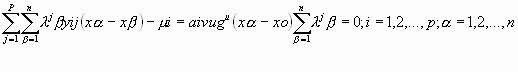[25]

donde Y_ij (xα - xβ) representa el semivariograma entre Z_i y Z_j para h = xα - xβ , los µ_i son los multiplicadores de Lagrange y g^u(xα - x₀) representa el valor de la u-ésima función básica g^u(h) entre el α-ésimo punto muestral y el punto x₀ donde se desea obtener la estimación. La condición de que la suma de los pesos sea cero significa que la media local de cada factor regionalizado también es igual a cero.

RESULTADOS Y DISCUSIÓN

El Cuadro 1 muestra la matriz de correlación de los promedios mensuales de precipitación observados en los 55 puestos pluviométricos del estudio durante el lapso 1968-1983. Estos valores describen la relación entre las variables en un mismo lugar (ver ecuación [6]). Los datos no pueden considerarse una muestra aleatoria porque están correlacionados espacialmente, por eso las típicas pruebas de significación carecen de validez. El alto grado de colinealidad presente en los promedios mensuales justifica la aplicación de un Análisis de Componentes Principales. Los resultados -obtenidos con el Sistema S-PLUS for Windows, versión 3.3 (1995)-, muestran que los tres primeros componentes explican el 85,8 % de la variación total representada por la matriz de varianza-covarianza de los doce promedios mensuales de precipitación.

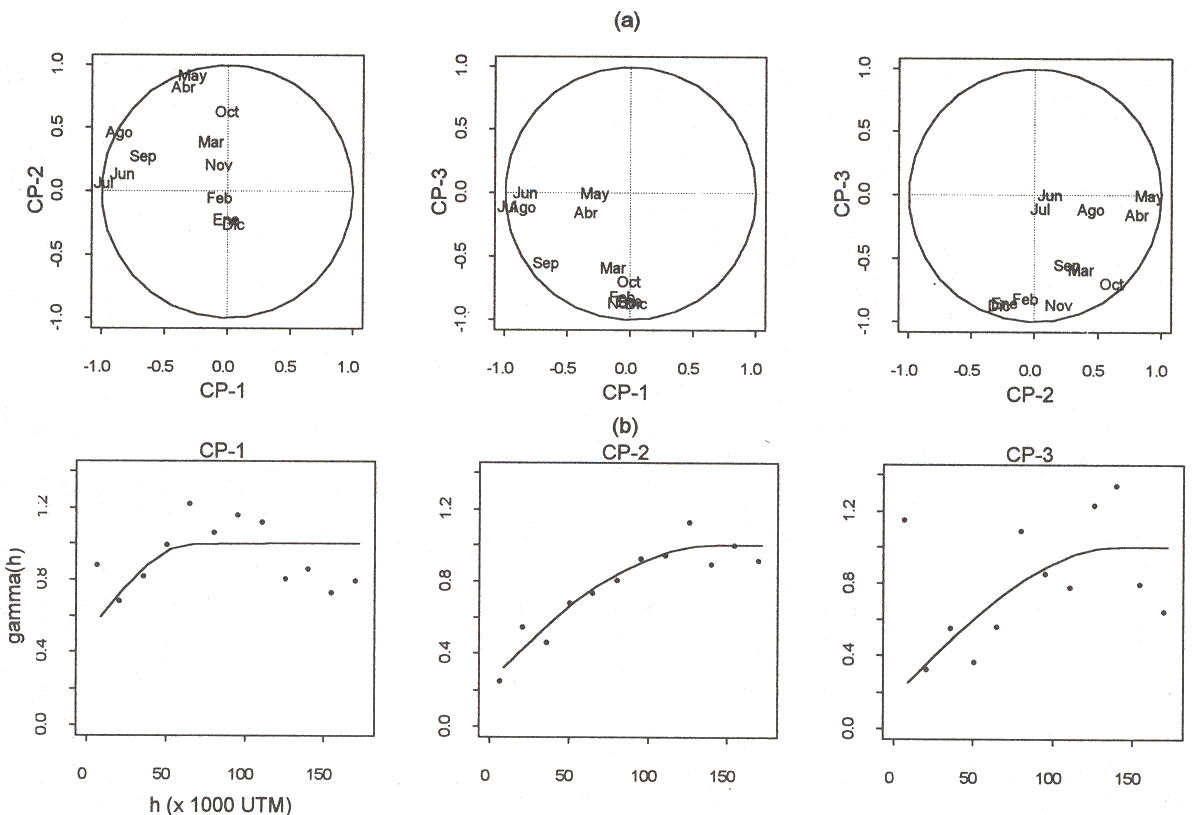
El círculo de correlaciones es un gráfico de la correlación entre las variables originales y un par de los primeros CP que permite resumir las relaciones entre las variables. Con el fin de facilitar la interpretación -y reducir la correlación espacial entre componentes a distancias cortas- se aplicó una rotación ortogonal de los tres primeros ejes principales utilizando un criterio varimax.

Los círculos de correlaciones de la Figura 1(a) permiten apreciar que el primer componente rotado está altamente correlacionado con la precipitación promedio durante junio, julio y agosto (época de lluvia), mientras que el tercer componente aparece fuertemente correlacionado con la precipitación promedio registrada entre noviembre y febrero (temporada seca). Meses de transición entre estaciones (abril, mayo y octubre) contribuyen al segundo componente.

El primer CP rotado, Y₁(xα), mostró el gradiente Norte -Sur que caracteriza el comportamiento del período lluvioso en la región estudiada, mientras que el segundo CP rotado, Y₂(xα), exhibió un gradiente Este-Oeste (Pradere, 1997a,b). Este efecto no estacionario se removió aplicando una regresión cuadrática sobre las coordenadas xα = (xα , yα) de cada punto de observación:

        = a_0,i + a_1,i xα + a_2,i xα ² + a_3,i yα + a_4,i yα ²      [26]

y estimando los semivariogramas sobre los residuales de la regresión { e_i,α = Y_i,α - ; i = 1, 2; α = 1, 2, ...,55 }. Para la estimación se utilizó el software de dominio público desarrollado por Bogaert et al. (1995), que utiliza como criterio de ajuste la minimización de una suma de cuadrados residual ponderada (WSS). Hasta el momento no se conoce la distribución teórica del estimador [9], de manera que no es posible realizar pruebas en un sentido estadístico. Utilizando una distancia de clase de 15 000 UTM y asumiendo isotropía (Y (h) = Y (׀h׀) = Y (h)), se obtuvo el mejor ajuste (WSS = 0,12159) mediante la suma de un efecto nugget y dos esquemas esféricos de la forma:

Y_ij (h) = b_ij¹ + b_ij² esf (h ; 65 000) + b_ij³ esf (h; 140 000); i, j = 1, 2, 3  [27]

donde:

esf (h; a) = 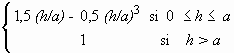             [28]

La Figura 1(b) muestra los semivariogramas experimentales simples (h) y los modelos Y_ii (h) ajustados a los tres primeros CP rotados. Para facilitar su comparación, ambas funciones han sido reducidas de manera que los semivariogramas simples estén principalmente dentro del intervalo [0,1]. El semivariograma del primer CP muestra el mayor efecto nugget y está dominado por la estructura esférica de rango más corto, mientras que los semivariogramas del segundo y del tercer componente exhiben un efecto nugget más reducido y parecen dominados por la estructura de mayor rango. Puesto que el primer componente caracteriza la precipitación promedio durante la temporada de lluvias, el análisis estructural parece indicar que este proceso tiene menor alcance espacial. El cambio de una estación a otra y la precipitación durante el período seco, fenómenos caracterizados por el segundo y el tercer CP, respectivamente, parecen tener un alcance espacial mayor. El marcado efecto nugget en el primer CP podría reflejar el carácter discontinuo de la precipitación a distancias muy cortas.

Figura 1: Círculos de correlaciones (a) y semivariogramas experimentales y teóricos simples reducidos (b) para los tres primeros componentes principales (rotados) de la matriz de varianza - covarianza.

El MLC ajustado permite estimar y mapear los tres primeros CP sobre una malla regular (Pradere, 1997a,b), pero aquí se utilizará sólo para identificar las estructuras de variabilidad espacial que modelarán la corregionalización de las doce variables originales. Se verá ahora la utilidad del AKF para descomponer la matriz V en S matrices B^u de corregionalización y apreciar si la estructura de correlación de estas últimas varía con la escala. Los principales factores regionalizados (obtenidos a partir de [24] y [25]) permitirán generar una clasificación de los patrones de precipitación de acuerdo con la escala de variación espacial.

Previamente al ajuste del Modelo Lineal de Corregionalización, se aplicó de nuevo regresión múltiple para remover tendencias. El ajuste se realizó mediante un software no comercial compuesto por subrutinas Fortran para usar bajo S-PLUS. Dada una matriz W semi-definida positiva y pesos positivos w(h_j), Goulard y Voltz (1992) definen como criterio para una distancia del tipo euclidiano el estadístico:

      WSS = w(h_j) traza [ (W (Γ(h_j) - (h_j) ))² ]         [29]

que proporciona una medida de la bondad del ajuste de Γ(h_j) a (h_j) para distintos incrementos h_j, con j=1, 2, ..., m. Generalmente los pesos w(h_j) son proporcionales a la cantidad de información utilizada por el estimador (por ejemplo, el número de pares) y W es la matriz identidad (métrica tipo 0), la matriz diagonal del inverso de las varianzas (métrica tipo 1) o la inversa de la matriz de varianza-covarianza (métrica tipo 2). Es importante notar que la distribución probabilística de [29] es desconocida y, por lo tanto, no puede hacerse una prueba en un sentido estadístico.

Para los doce promedios mensuales Z_i (xα) se propuso un MLC análogo a [27]:

Y_ij (h) = b_ij¹ + b_ij² esf (h; 65 000) + b_ij³ esf (h; 140 000); i, j = 1, 2, ..., 12 [30]

Los coeficientes de cada estructura generan las matrices de corregionalización B¹ = [b_ij¹], B² = [b_ij²] y B³ = [b_ij³]. Utilizando una métrica del tipo 2 (W = V^-1) se logró un ajuste razonable (WSS = 1,87819), lo que indica que la misma combinación de funciones básicas utilizadas para modelar la corregionalización de los tres primeros CP (rotados) de V genera un MLC adecuado para los promedios mensuales de precipitación.

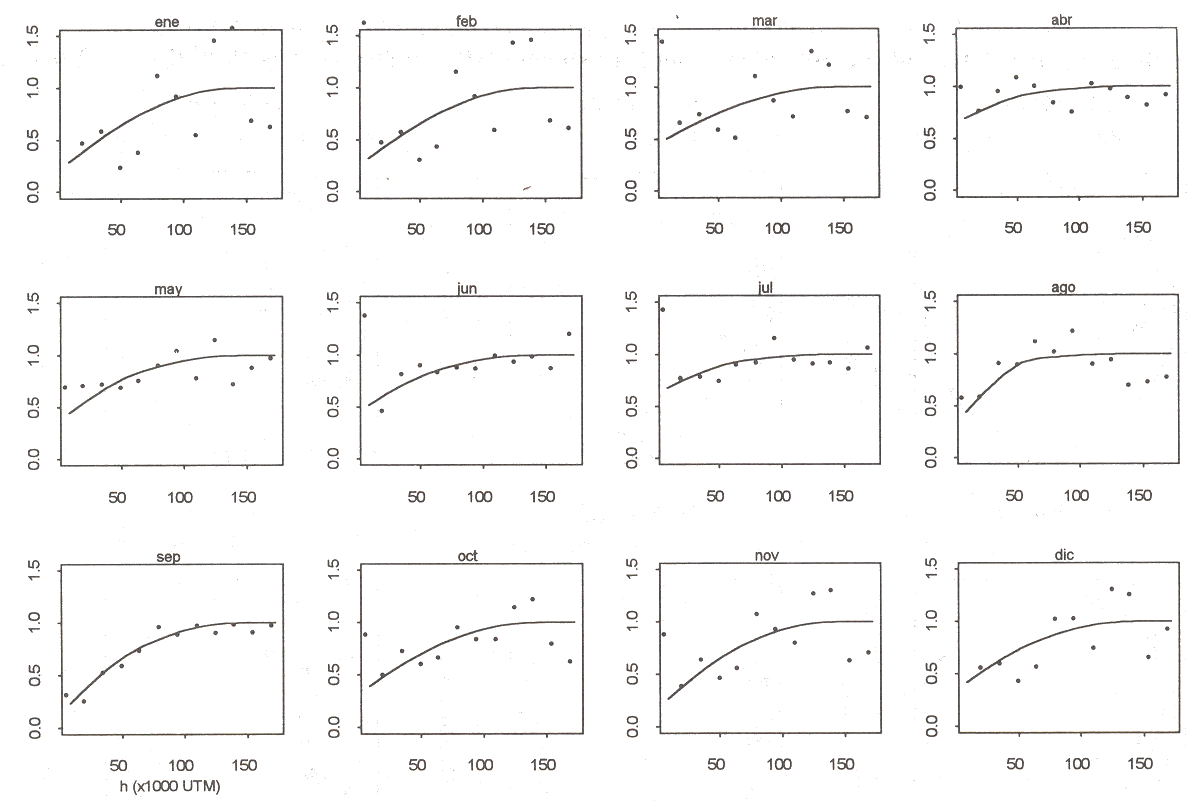
La Figura 2 muestra los semivariogramas simples experimentales (h) y teóricos Y_ii(h) para los promedios mensuales. De nuevo, ambas funciones aparecen reducidas al intervalo [0,1].

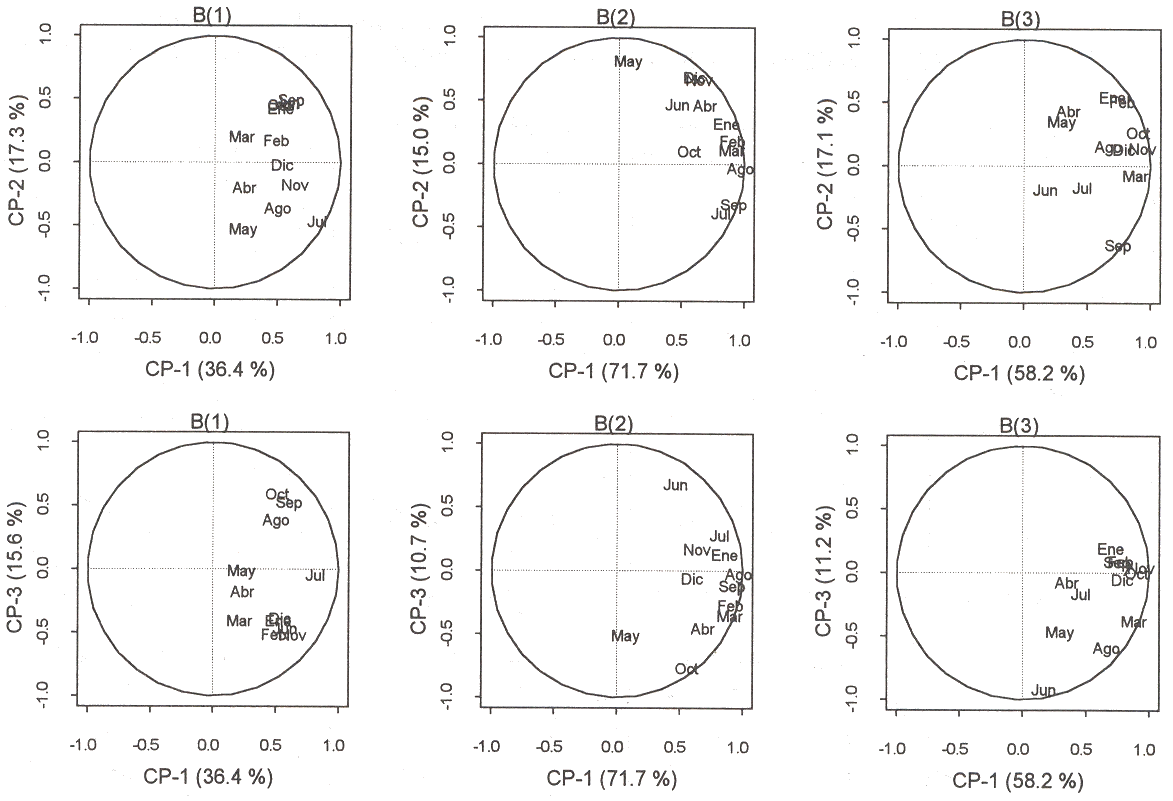
El efecto nugget es la estructura con mayor peso en los modelos ajustados a los promedios de abril, junio y julio, lo que indica que la precipitación promedio tiene un comportamiento menos continuo a distancias muy cortas durante estos meses. El coeficiente de la segunda estructura espacial (modelo esférico de rango igual a 65 000 UTM) tiene mayor peso en el modelo ajustado a la precipitación promedio de agosto. Para el resto de los promedios mensuales, la tercera estructura espacial (modelo esférico de rango igual a 140 000 UTM) es la más importante. Al aplicar un ACP a cada una de las tres matrices de corregionalización se encontró que los tres primeros componentes explicaban el 69,3 %, el 97,4 % y el 86,5 % de la variabilidad de B¹, B² y B³, respectivamente. La Figura 3 muestra los círculos de correlaciones para las tres matrices, con la inercia de cada componente indicada entre paréntesis.

Como se aprecia en la Figura 3, promedios relacionados con la temporada de lluvias están altamente correlacionados con el primer eje principal de B², la matriz que describe la correlación entre las variables a la escala de 65 000 UTM, mientras que los promedios relacionados con la estación seca están altamente correlacionados con el primer eje principal de B³, matriz asociada a la escala de 140 000 UTM. La precipitación promedio durante el mes de octubre (transición lluvia - sequía) muestra una alta correlación con el primer CP de B³ (estructura de rango largo), mientras que los promedios de abril y mayo (transición sequía - lluvia) están correlacionados con el primero y segundo ejes principales de B² (estructura de rango corto), respectivamente. Los tres primeros CP de B¹ -matriz asociada al efecto nugget- muestran una correlación de moderada a débil con la mayor parte de las variables; la mayor correlación ocurre entre el primer CP y el promedio de julio, el mes con componente nugget más importante.

Figura 2: Semivariogramas experimentales y teóricos simples reducidos para los doce promedios mensuales de precipitación.

Figura 3: Círculos de correlaciones para los tres primeros componentes principales de las matrices de corregionalización (la inercia de cada componente se indica entre paréntesis).

Los resultados muestran que la precipitación mensual promedio, descrita a partir de V mediante dos temporadas claramente definidas -lluviosa y seca- y la transición entre ellas, puede describirse también en términos de procesos que ocurren a diferentes escalas espaciales:

a. La estación lluviosa tiene, fundamentalmente, un carácter discontinuo a distancias muy cortas (efecto nugget) y correlación espacial de corto alcance (65 000 UTM).

b. Tanto la época de sequía como la transición de lluvia a sequía están influenciadas por la estructura de mayor rango espacial (140 000 UTM).

c. La transición de la temporada seca a la lluviosa está asociada, básicamente, a la estructura con rango espacial de 65 000 UTM.

El alcance espacial de los procesos de lluvia y sequía caracterizado antes fue parcialmente descrito a través de la matriz V. En cambio, la transición entre estaciones, que aparecía como un proceso único en el análisis previo, muestra una correlación espacial de corto rango en un sentido -seco a lluvioso y de rango mayor en sentido contrario -lluvioso a seco. Este comportamiento no pudo apreciarse en el ACP de V, donde ambos efectos están mezclados. Los resultados anteriores muestran cómo el AKF permite asociar a diferentes escalas de variación espacial aspectos de la estructura de correlación que están mezclados en V. La descomposición de V en matrices de corregionalización B^u permite definir el alcance espacial de cada uno de los procesos básicos de lluvia, sequía y transición entre estaciones identificados en el ACP de V.

Con el propósito de apreciar la influencia de la escala espacial, se estimaron los dos primeros factores regionalizados para cada una de las tres estructuras de variabilidad identificadas en el estudio. Puesto que para distancias superiores al rango de correlación espacial, el valor de cualquier factor regionalizado asociado a la u-ésima escala es igual a cero -su media local-, la estimación se limitó a los puntos muéstrales, ya que una malla regular habría generado un mapa difícil de interpretar. No se hará referencia a la precisión de las estimaciones porque, en el caso del kriging factorial, el cálculo de la varianza de estimación no es directo (Wackernagel, 1995).

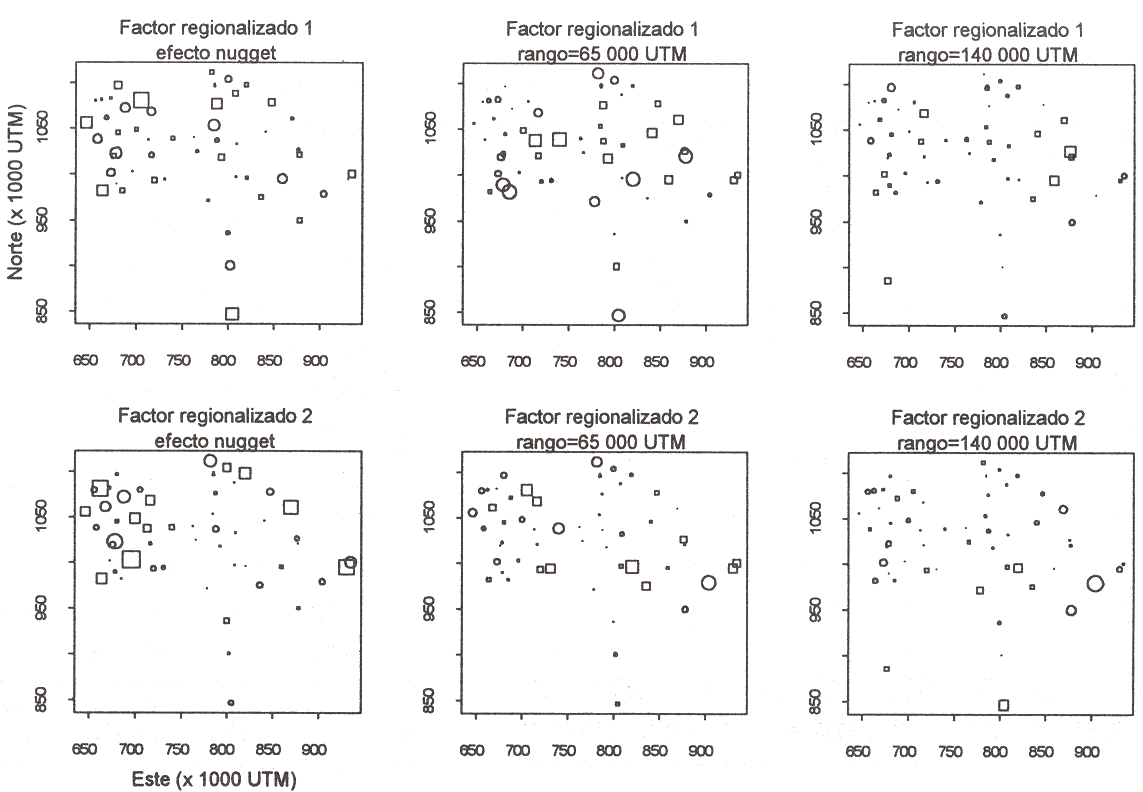
La Figura 4 muestra los factores regionalizados (xα) estimados en los puntos muéstrales para el efecto nugget (a) y para las escalas de 65 000 UTM (b) y 140 000 UTM (c). El área del símbolo utilizado (circular para valores positivos y cuadrado para valores negativos) es proporcional al valor estimado. Los puestos situados al Oeste y al Nor - Noreste parecen más influenciados por el efecto nugget, principalmente vinculado a la precipitación promedio durante el mes de julio. Al Centro y Centro- Este se observa variabilidad espacial a la escala de 65 000 UTM que, como se vio, aparece asociada al período lluvioso y a la transición sequía- lluvia. Finalmente, en algunos puestos situados al Este se aprecia el efecto de la escala de 140 000 UTM, vinculada a la temporada de sequía y al cambio lluvia - sequía.

Los dos primeros factores regionalizados estimados en los puntos muéstrales se utilizaron para generar una clasificación de los puestos pluviométricos según la escala de variación espacial. Por simplicidad, el valor estimado de cada factor se sustituyó por uno de tres niveles para representar valores inferiores a 0,5 (nivel 1), valores entre 0,5 y 0,5 (nivel 2), y valores mayores de 0,5 (nivel 3). Este procedimiento generó nueve grupos diferentes para cada escala:

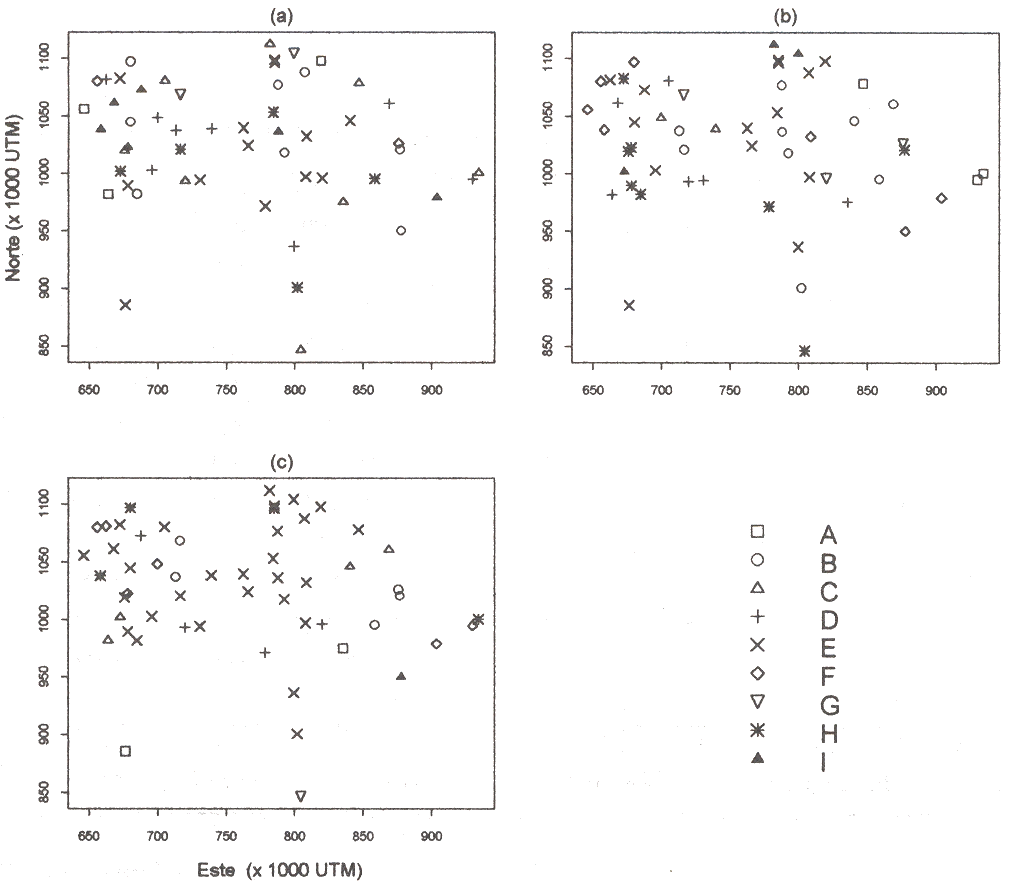
El Cuadro 2 muestra la clasificación para las tres escalas, y la Figura 5 muestra cómo la distribución de los grupos generados varía notablemente de una escala espacial a otra. Puesto que el nivel 2 representa valores alrededor del cero, la importancia de una escala particular en la variabilidad de la precipitación mensual promedio está dada por los niveles 1 y 3.

Figura 4: Mapas de los dos primeros factores regionalizados estimados en los puntos muéstrales. El área del símbolo utilizado (circular para valores positivos y cuadrado para valores negativos) es proporcional al valor estimado.

Figura 5: Clasificación de puestos pluviométricos en función de los dos primeros factores regionalizados: a) efecto nugget; b) 65 000 UTM; c) 140 000 UTM.

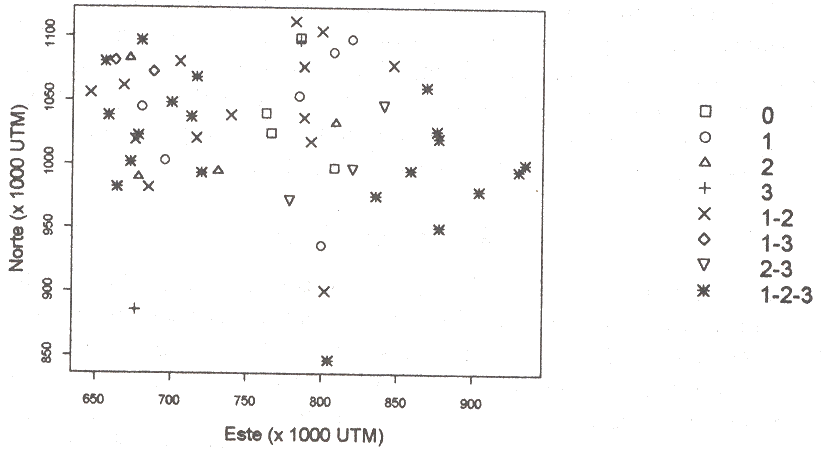
El Cuadro 3 resume la situación para cada puesto, y la Figura 6 muestra la distribución de puestos pluviométricos en función de la escala espacial dominante. La precipitación mensual promedio es el resultado de procesos dominados por las tres escalas espaciales en 20 puestos situados al Sur, Este y Oeste. En 14 puestos del Oeste y de un eje central Norte - Sur se observa el predominio de dos estructuras: el efecto nugget y la escala de 65 000 UTM, y en esa misma zona hay 6 puestos en los que el efecto nugget es la estructura espacial más importante. En la zona Centro- Norte ninguna de las tres estructuras parece tener influencia.

Figura 6: Clasificación de puestos pluviométricos en función de la escala espacial dominante (0 = ninguna; 1 = efecto nugget; 2 = 65 000 UTM; 3 = 140 000 UTM).

AGRADECIMIENTO

Esta investigación fue financiada por el Consejo de Desarrollo Científico y Humanístico de la Universidad Central de Venezuela a través del Proyecto CDCH Nº 08-11-3265/94, y cofinanciada por el Consejo de Investigación de la Facultad de Ingeniería de la UCV. La autora desea agradecer a la Dra. Lelys Bravo de Guenni (USB) por suministrar los datos que sirvieron de base para el análisis y al Dr. Michel Goulard (I.N.R.A., Francia) por proporcionar el software necesario para ajustar un Modelo Lineal de Corregionalización y estimar factores regionalizados. Igualmente a los revisores, por sus interesantes observaciones.

BIBLIOGRAFÍA

BOGAERT, P., P. MAHAU ; F. BECKERS. 1995. The spatial interpolation of agro-climatic data: cokriging software and source code. User's Manual, Version 1.0b. Rome: FAO Agrometeorology Series Working Paper, Number 12.

GOOVAERTS, P. 1992. Factorial kriging analysis: a useful tool for exploring the structure of multivariate spatial soil information. Jour. Soil Sci., v. 43, pp. 597-619.

GOOVAERTS, P. 1993. Spatial orthogonality of the principal components computed from coregionalized variables. Math. Geol., v. 25, n. 3, pp. 281-302.

GOOVAERTS, P. 1994. On a controversial method for modeling a coregionalization. Math. Geol., v. 26, n. 2, pp. 197-204.

GOOVAERTS, P.; P. SONNET; A. NAVARRE. 1993. Factorial kriging analysis of springwater contents in the Dyle River basin, Belgium. Water Resour. Res., v. 29, n. 7, pp. 2115-2125.

GOULARD, M.; M. VOLTZ. 1992. Linear coregionalization model: tools for estimation and choice of cross-variogram matrix. Math. Geol., v. 24, n. 3, pp. 269-286.

HEVESI, J.A.; J.D. ISTOK; A.L. FLINT. 1992a. Precipitation estimation in mountainous terrain using multivariate geostatistics: Part I: Structural analysis. J. Appl. Meteor., v. 31, pp. 661-676.

HEVESI, J.A.; J.D. ISTOK; A.L. FLINT. 1992b. Precipitation estimation in mountainous terrain using multivariate geostatistics: Part II: Isohyetal maps. J. Appl. Meteor., v. 31, pp. 677-688.

JOURNEL, A.G.; C.J. HUIJBREGTS. 1978. Mining geostatistics. Academic Press, London. 600 p.

MATHERON, G. 1971. The theory of the regionalized variables and its application. Cashiers du Centre de Morphologie Mathematique, No. 5. Ecole des Mines, Fontainebleau, France. 211 p.

MYERS, D.E. 1982. Matrix formulation of cokriging. Math. Geol., v. 14, pp. 249-257.

PRADERE, R. 1997a. Aplicación del análisis geoestadístico multivariado a la estimación y definición de patrones de precipitación en los llanos centrales venezolanos. Trabajo de Ascenso. Facultad de Ingeniería, Universidad Central de Venezuela.

PRADERE, R. 1997b. Definición de patrones de precipitación en los llanos centrales venezolanos mediante geoestadística multivariada. Memorias de la V Reunión de la Sociedad Internacional de Biometría para la Red de Centroamérica, el Caribe, México, Colombia y Venezuela. Xalapa, Veracruz, México. 6-9 de Agosto de 1997. pp. 166-177.

SOLOW, A.R.; S.M. GORELICK. 1986. Estimating monthly streamflow values by cokriging. Math. Geol., v. 18, n. 8, pp. 785-809.

Statistical Sciences, Inc. S-PLUS Guide to Statistical and Mathematical Analysis, Version 3.3 for Windows, Seattle: Statci, a division of MathSoft, Inc., 1995.

WACKERNAGEL, H. 1989. Description of a computer program for analyzing multivariate spatially distributed data. Comput. Geosci., v. 15, n. 4, pp. 593-598.

WACKERNAGEL, H. 1995. Multivariate geostatistics: an introduction with applications. Springer-Verlag, Berlin. 256 pp.

WACKERNAGEL, H.; C. BUTENUTH. 1989. Caractérisation d'anomalies géochimiques par la géostatistique multivariable. Jour. Geochem. Explor., v. 32, pp. 437-444.

WHITE D.; M. RICHMAN; B. YARNAL. 1991. Climate regionalization and rotation of principal components. Int. J. Climatol., v. 11, pp. 1-25.

^